Livre de recette sur l'étalonnage • gseries

Description des étapes d’un projet d’étalonnage typique avec G-Séries (librairie R gseries).

Autres ressources utiles liées au problème d’étalonnage de séries chronologiques discuté ici et résolu à l’aide des fonctions d’étalonnage de G-Séries (benchmarking() et stock_benchmarking()), par ordre croissant de complexité technique :

Fortier et Quenneville (2007), dans Références pour la fonction benchmarking(), pour une vue d’ensemble de la méthodologie de l’étalonnage de séries chronologiques implémentée dans G-Séries avec des exemples détaillés (en anglais seulement). Ce document est disponible dans GCdocs pour les employés de Statistique Canada (recherchez « ICES2007_Fortier.pdf » dans GCDocs).
Cours 0436, « Théorie et application de l’étalonnage », dans Références pour les fonctions benchmarking() et stock_benchmarking(). Consultez la page web Cours 0436 (site web grand public de Statistique Canada) pour plus de détails.
Dagum et Cholette (2006), dans Références pour la fonction benchmarking(), pour une discussion technique complète et une présentation des problèmes d’étalonnage de séries chronologiques et de leur solution (en anglais seulement).

1. Préparer les données d’entrée

La première étape consiste généralement à convertir les objets « ts » ou « mts » (librairie stats) dans le format approprié pour les fonctions d’étalonnage de G-Séries à l’aide des deux fonctions utilitaires suivantes ;

ts_to_tsDF() pour les séries indicatrices
ts_to_bmkDF() pour les étalons

Il est possible d’étalonner plusieurs séries en un seul appel aux fonctions d’étalonnage. Ceci peut être fait en spécifiant la liste appropriée des variables des data frames d’entrée avec les arguments var et with, ce qui peut être lourd à gérer et donner à votre code un aspect encombré. Une option plus pratique pour obtenir le même résultat serait d’utiliser l’argument allCols. Cependant, ces deux alternatives ont d’importantes limitations car elles requièrent toutes deux que toutes les séries indicatrices soient de la même longueur (même nombre de périodes) et aient le même ensemble (nombre) d’étalons. Les valeurs des étalons peuvent évidemment différer pour chaque série indicatrice, mais leur couverture doit être la même.

Une approche plus souple, qui ne souffre pas des limitations mentionnées ci-dessus, consiste à utiliser le mode groupes-BY (argument by) des fonctions d’étalonnage après avoir converti les data frames d’entrée en versions empilées (longues) à l’aide des fonctions utilitaires suivantes :

stack_tsDF() pour les séries indicatrices
stack_bmkDF() pour les étalons

Les versions empilées des data frames n’utilisent que deux variables pour spécifier les informations concernant les différentes séries indicatrices ou séries d’étalons : une variable pour les identifiants et une autre pour les valeurs. Un data frame empilé contient donc plus d’enregistrements (lignes) mais moins de variables (colonnes) qu’un data frame non empilé, les séries chronologiques étant empilées les unes sur les autres au lieu d’être étalées les unes à côté des autres. Le traitement groupes-BY avec des data frames empilés est l’approche recommandée pour étalonner plusieurs séries en un seul appel à la fonction d’étalonnage, à moins que le nombre de séries à comparer soit extrêmement important et que le temps de traitement soit une question vraiment cruciale (le traitement de séries chronologiques multiples avec les arguments var ou allCols devrait être légèrement plus rapide que l’approche groupes-BY avec l’argument by).

2. Effectuer l’étalonnage

Le nombre d’appels aux fonctions d’étalonnage dépend des valeurs des arguments rho, lambda, biasOption et bias (plus low_freq_periodicity, n_low_freq_proj et proj_knots_rho_bd pour la fonction stock_benchmarking()). Un appel est nécessaire pour chaque combinaison distincte des valeurs de ces arguments. En pratique, cependant, seul l’argument lambda nécessitera habituellement des valeurs distinctes pour traiter l’ensemble des séries : lambda = 1 pour un étalonnage proportionnel et lambda = 0 pour un étalonnage additif. Deux appels aux fonctions d’étalonnage sont donc souvent suffisants.

Lorsque plus d’un appel est nécessaire, les data frames d’entrée pour les séries indicatrices est les étalons doivent être divisés en data frames distincts : un pour chaque appel avec l’ensemble pertinent de séries indicatrices et d’étalons. Il est également possible d’ajouter une ou plusieurs colonnes aux versions empilées des data frames d’entrée afin d’identifier (et d’extraire) les séries indicatrices et les étalons de chaque appel.

Note sur l’étalonnage proportionnel et additif
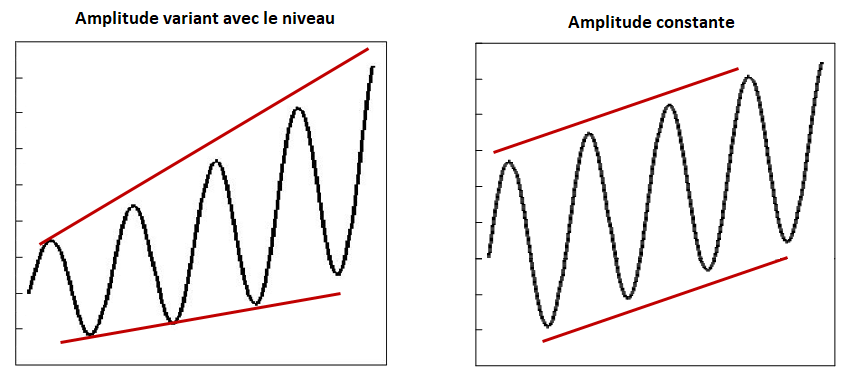
L’étalonnage proportionnel (\lambda \ne 0) est normalement utilisé lorsque l’objectif principal est la préservation des ratios (différences relatives) d’une période à l’autre et l’étalonnage additif (\lambda = 0) pour la préservation des différences. Il est généralement préférable de privilégier l’analyse des ratios d’une période à l’autre pour les séries chronologiques dont l’amplitude (ex., les composantes saisonnières et irrégulières) varie selon le niveau de la série. En revanche, si l’amplitude de la série reste relativement constante quel que soit le niveau de la série, il convient d’examiner les différences d’une période à l’autre.

Amplitude de la série

L’erreur la plus courante serait probablement l’utilisation d’une approche d’étalonnage additif lorsque les changements dans l’amplitude de la série d’indicateurs sont importants et suivent le niveau (l’amplitude augmente/diminue avec le niveau). Le principal avantage de l’étalonnage additif est qu’il fonctionne (retourne une solution) dans tous les contextes, alors que l’étalonnage proportionnel échouera dans certains cas particuliers (ex., un étalon non nul avec des valeurs de série indicatrice nulles pour toutes les périodes couvertes par l’étalon). L’étalonnage proportionnel avec \rho < 1 (étalonnage basé sur la régression) fonctionne généralement bien dans la pratique (fournit des solutions raisonnables) avec des problèmes impliquant des valeurs de zéro pour les séries indicatrices et/ou les étalons. Certaines personnes peuvent en fait apprécier (trouver attrayant) le fait que les valeurs de zéro dans la série indicatrice initiale demeurent zéro dans les séries étalonnées de manière proportionnelle, ce qui n’est pas le cas pour les séries étalonnées de manière additive. En ce qui concerne l’étalonnage proportionnel avec \rho = 1 (étalonnage de Denton), la série indicatrice doit être strictement positive. Cependant, on peut essayer d’utiliser l’argument constant afin d’ajouter une constante temporaire (relativement petite) aux données d’entrée et ainsi résoudre les cas qui impliquent des valeurs de zéro dans la série indicatrice. En pratique, on notera que l’étalonnage proportionnel de Denton peut également être approximé avec l’approche basée sur la régression en utilisant une valeur de \rho inférieure à, mais très proche de, 1.0 (par exemple, \rho = 0.999). Enfin, bien que l’étalonnage proportionnel (\lambda \ne 0, \forall \rho) ne soit pas possible par défaut en présence de valeurs négatives, ce comportement peut être modifié avec l’argument negInput_option. Dans tous les cas, il convient de surveiller de près les séries étalonnées de manière proportionnelle impliquant des valeurs négatives ou des valeurs de zéro (ou presque zéro), où les ratios peuvent être indéfinis, instables ou difficiles à interpréter. Les données étalonnées de manière proportionnelle qui en résultent doivent être soigneusement analysées et validées dans de tels cas pour s’assurer qu’elles correspondent à des solutions raisonnables et interprétables.

3. Valider les résultats

Tout message d’avertissement ou d’erreur généré par les fonctions d’étalonnage doit être examiné afin de résoudre le(s) problème(s) correspondant(s). Une fois que l’on a obtenu des exécutions propres des fonctions d’étalonnage (sans messages d’avertissement ou d’erreur), il faut valider les données des séries étalonnées qui en résultent. La fonction utilitaire plot_graphTable() génère des graphiques utiles pour réaliser cette tâche.

Exemples d’éléments à rechercher dans les résultats d’étalonnage :

Ajustements d’étalonnage projetés inadéquats. La solution de l’étalonnage pour les périodes non couvertes par un étalon en fin de série est déterminée par le paramètre \rho (argument rho) et la correction pour le biais (spécifiée avec les arguments biasOption et bias). La correction du biais est généralement recommandée lorsque le niveau des étalons et des valeurs de la série indicatrice sont systématiquement différents (ex., les étalons sont toujours, ou presque toujours, plus grands que la série indicatrice ou vice versa). Le fait de ne pas corriger un biais (important) peut entraîner de mauvais résultats pour les périodes non couvertes par un étalon (ajustements d’étalonnage projetés inadéquats), ce qui peut ensuite conduire à d’importantes révisions lorsque de nouveaux étalons seront disponibles à l’avenir. La correction du biais devrait aider dans de tels cas. Une exception est l’étalonnage de Denton (\rho = 1) où la correction du biais n’a pas d’impact sur la solution de l’étalonnage. La modification de la valeur du paramètre \rho, qui détermine la vitesse à laquelle les ajustements projetés convergent vers le biais pour les périodes non couvertes par un étalon, peut également améliorer la situation. Plus la valeur de \rho est petite, plus la convergence est rapide, avec une convergence immédiate lorsque \rho = 0 et pas de convergence du tout (l’ajustement de la dernière période couverte par un étalon est répété) lorsque \rho = 1 (étalonnage de Denton). Une recommandation générale qui fonctionne raisonnablement bien dans la plupart des cas est d’ajuster avec le biais moyen estimé (biasOption = 3 et bias = NA) et d’utiliser \rho = 0.9 avec des indicateurs mensuels et \rho = 0.9^3 = 0.729 avec des indicateurs trimestriels. La spécification d’un biais défini par l’utilisateur (argument bias) peut être pertinente si les écarts entre les deux sources de données ont évolué dans le temps (ex., spécifier une valeur plus représentative du biais récent). Une autre solution consisterait à utiliser des prévisions explicites pour les étalons en fin de série au lieu de s’appuyer sur les étalons projetés implicites associés à l’ajustement du biais et au paramètre \rho. Par exemple, des informations auxiliaires disponibles pourraient être utilisées pour générer des étalons explicites et (si les prévisions sont bonnes) réduire les révisions une fois que les vraies valeurs des étalons seront connues. Les deux premiers graphiques d’étalonnage (Original Scale Plot et Adjustment Scale Plot) de la fonction plot_graphTable() devraient aider à identifier les problèmes potentiels avec les projections.
Paramètre autorégressif \rho (argument rho) inadéquat. L’objectif de l’étalonnage est généralement de préserver les mouvements de période à période de la série indicatrice, ce qui correspond à des valeurs de \rho relativement proches de 1 et à des ajustements d’étalonnage lisses. Ceci étant dit, certains cas particuliers peuvent justifier de faibles valeurs de \rho correspondant à des ajustements moins lisses et une préservation du mouvement plus faible. Le 2^e graphique d’étalonnage (Adjustment Scale Plot) de la fonction plot_graphTable() montre les ajustements d’étalonnage et peut donc être utilisé pour vérifier le « caractère lisse » des ajustements et modifier, si nécessaire, la valeur du paramètre \rho. Le degré de préservation du mouvement correspondant est illustré par les 3^e et 4^e graphiques d’étalonnage (Growth Rates Plot et Table) de la fonction plot_graphTable(). Notez que les ajustements d’étalonnage peuvent également être tracés en utilisant la fonction utilitaire plot_benchAdj().
Paramètre du modèle d’ajustement \lambda (argument lambda) inadéquat. L’étalonnage additif est mis en œuvre lorsque \lambda = 0 et l’étalonnage proportionnel dans le cas contraire (lorsque \lambda \ne 0). Le choix du modèle d’ajustement idéal n’est pas nécessairement évident. Se référer à la Note sur l’étalonnage proportionnel et additif ci-dessus pour en savoir plus. Essayer les deux approches d’étalonnage et comparer les graphiques d’étalonnage peut aider à choisir le modèle d’ajustement le plus adéquat. Par exemple, l’approche qui génère une série d’étalonnage d’apparence plus naturelle dans le 1^er graphique (Original Scale Plot), des ajustements d’étalonnage plus lisses dans le 2^e graphique (Adjustment Scale Plot) et une meilleure préservation du mouvement dans les 3^e et 4^e graphiques (Growth Rates Plot et Table) devrait être privilégiée. L’examen des graphiques d’étalonnage de la fonction plot_graphTable() devrait également permettre d’identifier les solutions problématiques qui pourraient nécessiter un changement de modèle d’ajustement. Par exemple, les cas problématiques d’étalonnage proportionnel avec des valeurs négatives (voir l’argument negInput_option) ou des valeurs nulles ou presque nulles pour les étalons ou les séries indicatrices risquent fort probablement de générer des séries étalonnées d’apparence suspecte dans le 1^er graphique (Original Scale Plot), des ajustements extrêmes ou non lisses dans le 2^e graphique (Adjustment Scale Plot) ou une mauvaise préservation des mouvements dans les 3^e et 4^e graphiques (Growth Rates Plot et Table). Un étalonnage additif peut être une meilleure alternative dans de tels cas.

Porter un regard attentif à tous les graphiques n’est pas nécessairement réalisable en pratique pour les grands projets d’étalonnage impliquant de nombreuses séries. Une analyse de classification (grossière) des données du data frame de sortie graphTable des fonctions d’étalonnage (l’entrée de la fonction plot_graphTable()) peut aider à identifier les cas nécessitant une investigation plus poussée et un regard plus attentif aux graphiques d’étalonnage.

Note sur les séries de stocks
L’étalonnage de séries de stocks avec la fonction benchmarking() génère des ajustements non lisses (« bris » dans les ajustements) autour de chaque étalon, quelles que soient les valeurs de \rho et de \lambda. Ceci est dû à la nature des étalons, c’est-à-dire des valeurs discrètes couvrant une seule période (points d’ancrage). La fonction stock_benchmarking(), spécifiquement destinée à l’étalonnage des séries de stocks, fournit généralement de meilleurs résultats (c.-à-d., une meilleure préservation des mouvements et des ajustements plus lisses). La fonction plot_benchAdj() est particulièrement utile pour comparer (superposer) les ajustements de séries de stocks générés par les fonctions benchmarking() et stock_benchmarking().

4. Traiter les données étalonnées

L’étape finale consiste généralement à convertir les données étalonnées (data frame de sortie series des fonctions d’étalonnage) en objets « ts » (ou « mts ») avec la fonction utilitaire tsDF_to_ts(). Lorsqu’un traitement par groupes-BY (argument by) est utilisé, il faut d’abord désempiler les données des séries étalonnées en utilisant la fonction utilitaire unstack_tsDF() avant d’appeler la fonction tsDF_to_ts().

Étalons non contraignants (nonbinding benchmarks)
Bien que les problèmes d’étalonnage impliquant des étalons non contraignants (coefficients d’altérabilité supérieurs à 0) soient relativement rares en pratique, il est important de se rappeler que le data frame de sortie benchmarks des fonctions d’étalonnage contient toujours les étalons originaux (non modifiés) fournis en entrée. Dans de tels cas, les étalons non contraignants modifiés seraient récupérés (calculés) à partir du data frame de sortie series. Par exemple, les flux étalonnés résultant d’un appel à benchmarking() peuvent être agrégés en utilisant la fonction stats::aggregate.ts() après avoir d’abord converti le data frame de sortie series en un objet « ts » avec la fonction utilitaire tsDF_to_ts().